在科研、教育以及工程领域,将复杂的数学公式从 PDF 或照片中提取出来并转化为可编辑的 $LaTeX$ 格式,一直是一项让人头疼的“体力活”。从早期的规则匹配到后来的深度学习模型,OCR 技术在处理数学符号时总是显得捉襟见肘。
然而,GOT-OCR 2.0 的出现,凭借其强大的序列生成能力和对空间结构的极致理解,彻底改变了这一现状。它不再只是简单地“认字”,而是像数学家一样在“理解”公式。
一、 为什么数学公式是 OCR 的“天敌”?
数学公式识别(Formula Recognition)之所以比普通文字识别难,主要由于以下三个特性:
- 二维空间结构: 不同于水平排列的文本,公式中充满了上标、下标、分数线、根号以及矩阵。
- 符号极其相似: 在模糊的图像中,字母 $v$ 与希腊字母 $\nu$、数字 $0$ 与字母 $O$、甚至求和符号 $\sum$ 与积分符号 $\int$ 极易混淆。
- 嵌套深度: 一个复杂的分式中可能嵌套着根式,根式里又嵌套着指数函数。传统的 OCR 在处理这种递归结构时,往往会发生“逻辑崩溃”。
二、 GOT-OCR 的“数学天赋”:三项核心利器
GOT-OCR 2.0 在数学表现上之所以惊艳,核心在于它打破了传统 OCR 的局限性。
1. 原生 $LaTeX$ 序列生成
不同于将公式切碎识别再拼接,GOT-OCR 采用端到端的转换机制。它直接将视觉特征映射为标准的 $LaTeX$ 字符串。这意味着模型在训练阶段就学习到了数学语言的“语法”,从而能自发地修正由于图像模糊导致的结构错误。
2. 对长公式与分段公式的超强鲁棒性
在处理跨行的长公式或大型矩阵时,GOT-OCR 表现出了极高的稳定性。它能精准识别矩阵的行列对齐关系,即便是在手机拍摄的倾斜、反光环境下,也能保持极高的转录准确率。
3. “视觉推断”补全缺失
得益于大规模预训练,当公式中的某个符号被污渍遮挡时,GOT-OCR 能根据上下文逻辑进行推断。例如,在一个积分号 $\int$ 后面,如果出现了一个模糊的符号,模型会优先将其推断为变量 $dx$。
三、 实战:GOT-OCR 的公式转化效果对比
为了直观感受 GOT-OCR 的威力,我们来看几个典型的转换场景:
场景 A:高阶导数与极限
- 输入: 包含分式、极限符号 $\lim$ 和高阶偏导数的模糊截图。
- GOT-OCR 输出:
- 评价: 完美识别了下标的趋近符号和分式的层级关系。
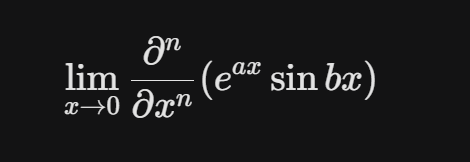
场景 B:大型矩阵与向量
- 输入: 带有括号嵌套的 $3 \times 3$ 矩阵。
- GOT-OCR 输出:使用标准
\begin{pmatrix} ... \end{pmatrix}环境,自动完成行列对齐,无需人工二次排版。
四、 如何在 Python 中调用 GOT-OCR 进行公式提取?
利用开源社区提供的工具,你可以轻松地将 GOT-OCR 集成到你的学术工作流中:
Python
from transformers import AutoModel, AutoTokenizer
import torch
# 加载 GOT-OCR 2.0 模型 (示例路径)
model_name = "stepfun-ai/GOT-OCR2_0"
model = AutoModel.from_pretrained(model_name, trust_remote_code=True).cuda().eval()
tokenizer = AutoTokenizer.from_pretrained(model_name, trust_remote_code=True)
def ocr_math_formula(image_path):
# 使用专门的提示词告知模型处理公式任务
res = model.chat(tokenizer, image_path, ocr_type='format', render=True)
return res
# 示例:提取并打印 LaTeX
latex_code = ocr_math_formula("calculus_hw.png")
print(f"提取出的 LaTeX 代码: {latex_code}")
五、 结语:科研人员的“救星”
GOT-OCR 2.0 的数学表现,不仅是技术上的秀肌肉,更是生产力的巨大解放。它让“手写草稿变论文代码”成为了可能,极大地缩短了学术成果从纸面到电子文档的距离。